Further Symmetry In Primes
2022-10-08 |
Using two distinct rule for generating primes
Two disjoint (?) sets of primes can be generated using two distinct rules:
$$ P' = \{f(3p - 2)\}$$
$$ P'' = \{f(6p - 1)\}$$
where \(p\) is prime and \(f\) is a function to select only prime numbers
We can calculate the ratio
$$\frac{P''}{P'}= \frac{6p - 1}{3p-2}$$
which tends to \(2\) as \(p\) tends to infinity
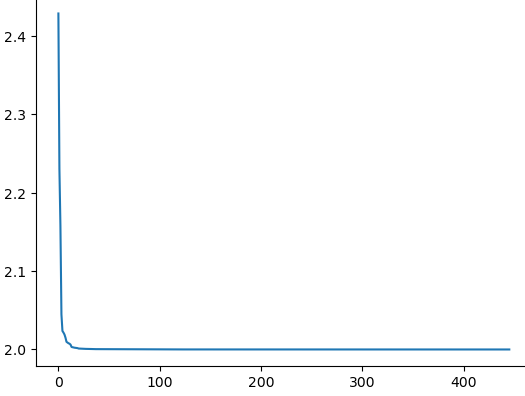
The largest prime tested is:
$$p = 1159337; p' = 3478009; p" = 6956021$$
with ratio: \(2.00000086256246\)