LƦ | Ʀamblings

All Linear Functions Are Injective: Proof By Contradiction (Geometrical)

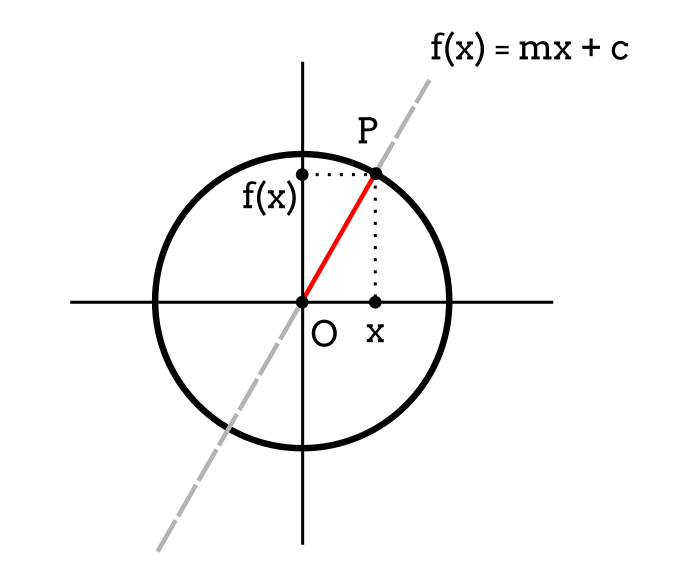
Showing that linear functions are injective is trivial, but using a proof by contradiction bringing up geometry is fascinating. After all, what really matters is the journey, not the destination!

We first bring up the definition of injective function

$$f(a)=f(b) \implies a = b \tag{1}$$

This can then be negated (with some preparation). Indeed, \((1)\) is equivalent to

$$f(a)\not = f(b) \lor a = b$$

We then negate it

$$\neg (f(a)\not = f(b) \lor a = b)$$

Which leads to the final form

$$(f(a) = f(b)) \land (a \not = b) \tag{2}$$

At this point, we'll assume \((2)\) as true and attempt to show that it is false, which will prove that \((1)\) is true.

Additional preparatory steps are required to setup the geometrical framework in which we'll prove \((1)\).

In figure 1 we see the graph of a general linear function of the form

$$y = mx + c \tag{3}$$

The major constraint to impose on \((3)\) is that $$m \not= 0$$

We then find two points \(O,P\) on the line at a distance of 1 unit from each other. Then, we trace a circle with radius \(OP\) and center in \(O\). This is a unit circle on \(P\) and this whole procedure is required to temporarily suppress the constant term \(c\) (similar to adding \(-c\) to the equation of the line).

We next find the slope of \((3)\) by taking advantage of the coordinates of the point P on the unit circle.

$$P=(x, f(x))$$

$$m = f(x)/x$$

According to \((2)\) \(a \not = b\), so we can express \(b\) as:

$$b = (a + \epsilon), \forall \epsilon \in \mathbb{R} \land \epsilon \not= 0$$

I want to highlight this constraint as it is crucial to the proof

$$\epsilon \not= 0 \tag{5}$$

According to \((2)\) we can plug either \(a\) or \(b\) into \((2)\) to get the same output, so

$$f(a) = ma$$

$$f(a + \epsilon) = m(a + \epsilon)$$

However, according to \((2)\) we know that \(f(a) = f(a+\epsilon)\) so we can let

$$ma = m(a + \epsilon)$$

Canceling out \(m\), with \(m\not= 0\), we are left with

$$a = a + \epsilon \tag{5}$$

At this point, the only way to make statement \((5)\) true is to assume that \(\epsilon = 0\) but this leads to a contradiction with \((4)\). Therefore we reject \((2)\) and we prove that \((1)\) is true \(\square\)